塾長が過去問を解くコーナーです!
前回は2021年の高専過去問(追試験)を解いていますね!
本試験は解説が豊富だと思うので今回も追試験の問題を解いていくことにします!
さっそく追試験の過去問を解いてみよう
しっかりプリントで解きたい方は、高専の公式ホームページからダウンロードできます。
それでは1番から順に解いていきましょう!
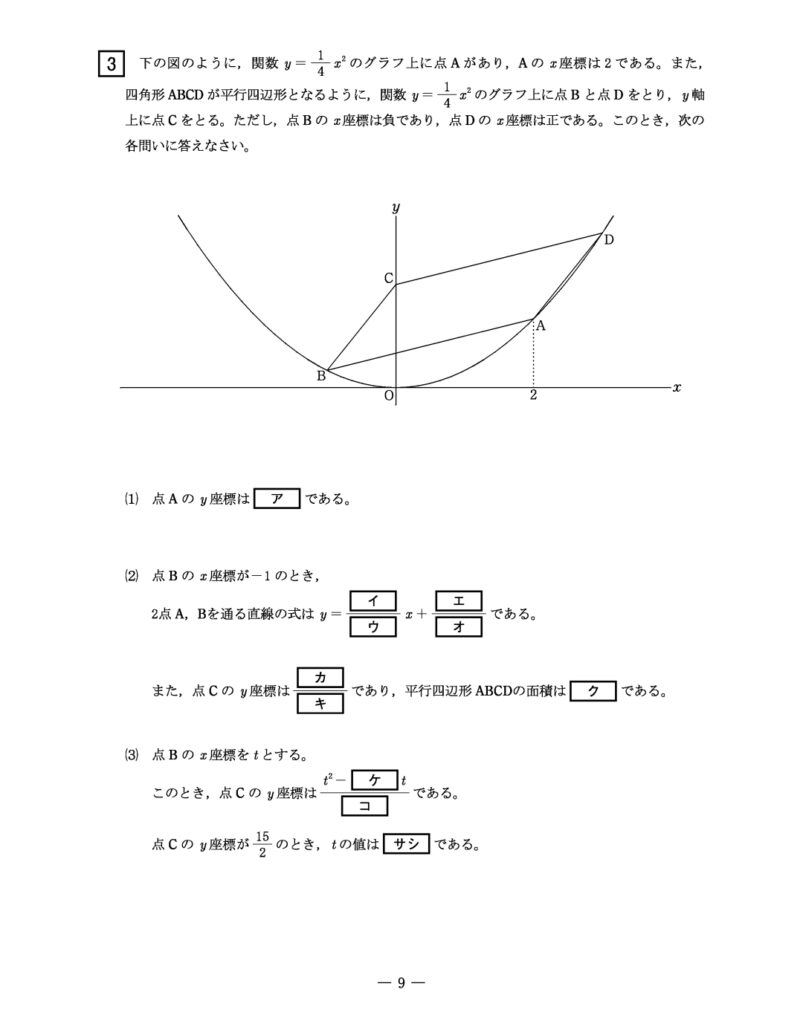
⑴関数の基礎的な問題
点Aのy座標を求める問題ですね。
関数y=1/4x² の式にⅹ=2を代入。
⑵直線の式を求める(前編)
ここも前半は、一次関数の直線の式を求める基礎的な問題です。
「放物線の比例定数」が分かっている場合はカンタンに求めることが出来るので公式を知らない人は覚えておきましょう。
・2点A、Bを通る直線の傾き
放物線の比例定数 ×(左のx座標+右のx座標)
1/4×(-1+2) = 1/4
・2点A、Bを通る直線の切片
放物線の比例定数(マイナス)×左のx座標×右のx座標
-1/4×(-1)×2 = 1/2
✅ イ=1 ウ=4 エ=1 オ=2
⑵点Cのy座標と平行四辺形の面積を求める
まず点Cのx座標が、点Bのx座標から左に1つだけ進んでいることに気づく。
すると点Dの座標が(3、9/4)というのが分かる。
平行四辺形の向かい合う直線の傾きは等しいので、点Bのy座標に5/4を足して点Cのy座標は3/2。
平行四辺形の面積は左から三角形、台形、三角形に分割してそれぞれを求積して足せば確実に出せる。
入試ではカンタンに求める方法を考えすぎないことも攻略のコツとなる。
✅ カ=3 キ=2 ク=3
⑶文字を使って座標を表す
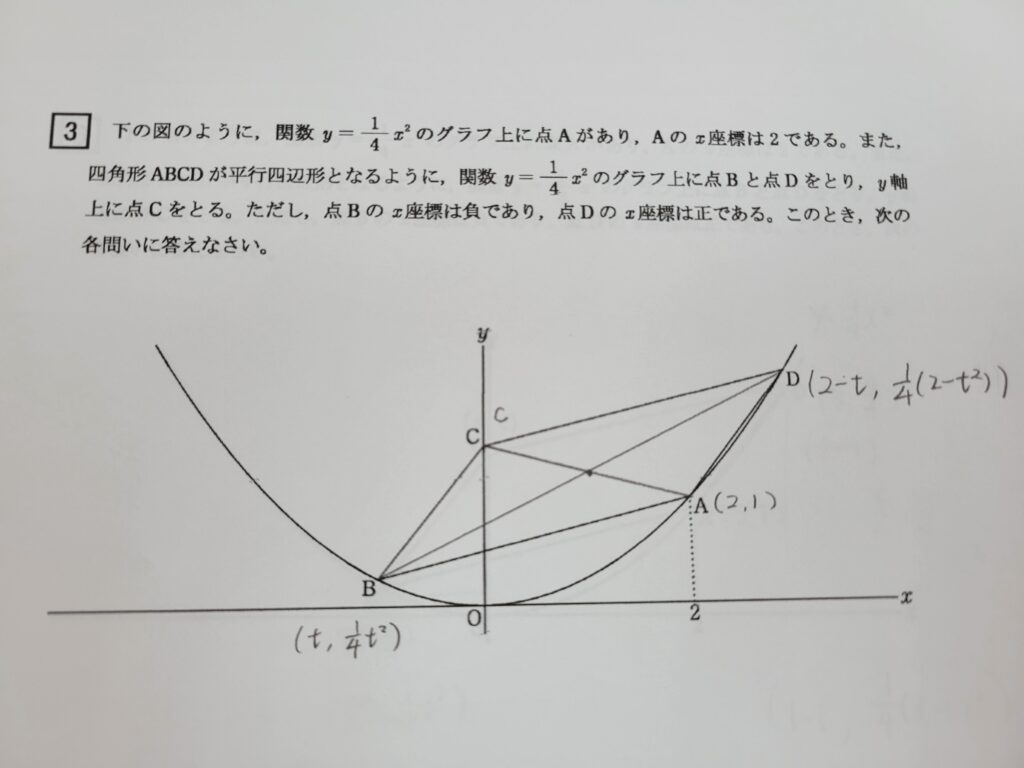
まずは点Dの座標をtを使って表すことが思いつくはず。
点D=(2-t、1/4(2-t)²)
平行四辺形の対角線の交点は、それぞれ中点になることを利用して解く。
つまり、「対角線BDの交点と対角線CAの交点の座標はそれぞれ中点が同じになる」という方程式を作る。
{1/4(2-t)²-1/4t²}/2 = (C+1)/2
これを解くと、
C=t²-2t/2
点Cのy座標に15/2を代入して、tの値は-3になる。
✅ ケ=2 コ=2 サシ=-3
まとめ
高専の関数の問題は、処理が大変だが比較的取りやすい問題が多いのでたくさん練習して確実に得点できるようにしておきましょう!















✅ ア=1