今回も高専の追試験の過去問を解説したいと思います。
他の年度の過去問解説はこちらをご覧ください。
幾何の問題は柔軟な発想力が必要!
早速問題を解いていきたいと思います!
高専の幾何は特に「柔軟な発想力」が問われるので、問題を数多く解くのをオススメします。
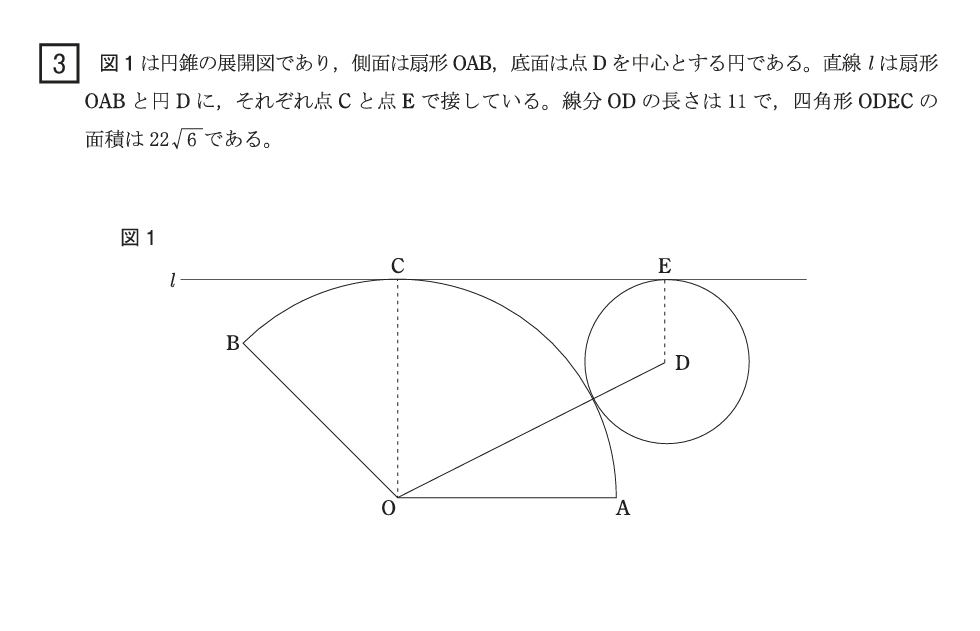
(1) OC+DE=□
OCとDEは、よく見るとそれぞれの円の半径。
なのでOC+DE=ODより、11
(2) CE=□√□
(1)が誘導問題になっているので、これを利用する。
CEをaとおくと、四角形ODECは台形より、
11×a×1/2=22√6
11a/2=22√6
a=4√6
よってCE=4√6
(3) DE=□
ここから難易度が上がる。
下図のように、先ほど求めたCEを移動させて、
△ODFで三平方。
11²=4√6²×□²
□=5
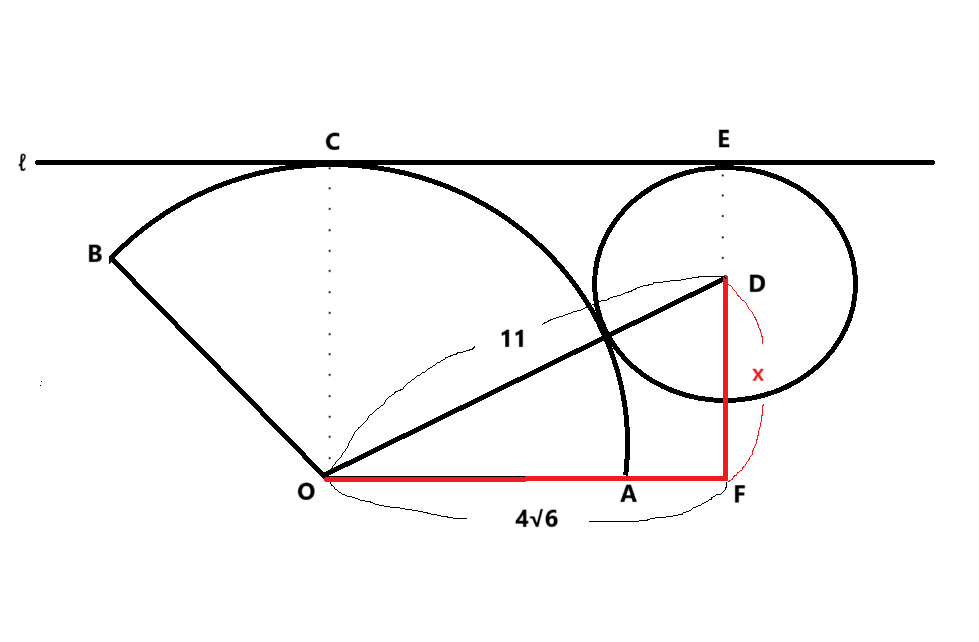
次に、△ODFの面積を求めると、
4√6×5×1/2=10√6
四角形ODECの面積は22√6なので、四角形OCEFの面積は32√6になった。
四角形の面積は縦×横なので、32√6÷4√6でOC=8
8-5で、DE=3
(4) ∠AOB=□°
おうぎ形の母線と底面の半径が分かったので、円錐のおうぎ形部分の中心角を求める公式を使う。

x/360=r/ℓより、
x/360=3/8
x=135°
(5) 切り口の面積
焦らなければ解ける問題。点線が相似形を示唆している。
円錐の中に球が入っている問題は、
「円外の1点からその円に引いた2本の接線の長さは等しい」という性質を利用することが多い。
前問から、
底面の半径は3、おうぎ形の母線は8なので、下図のようになる。
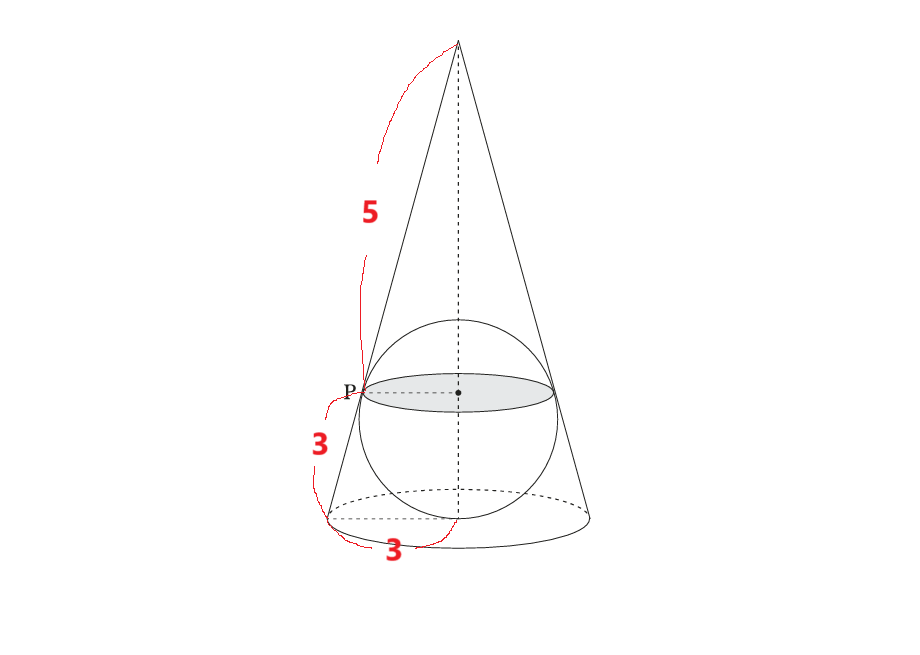
空間を平面においたときに、下図のように8対5の相似形になる。
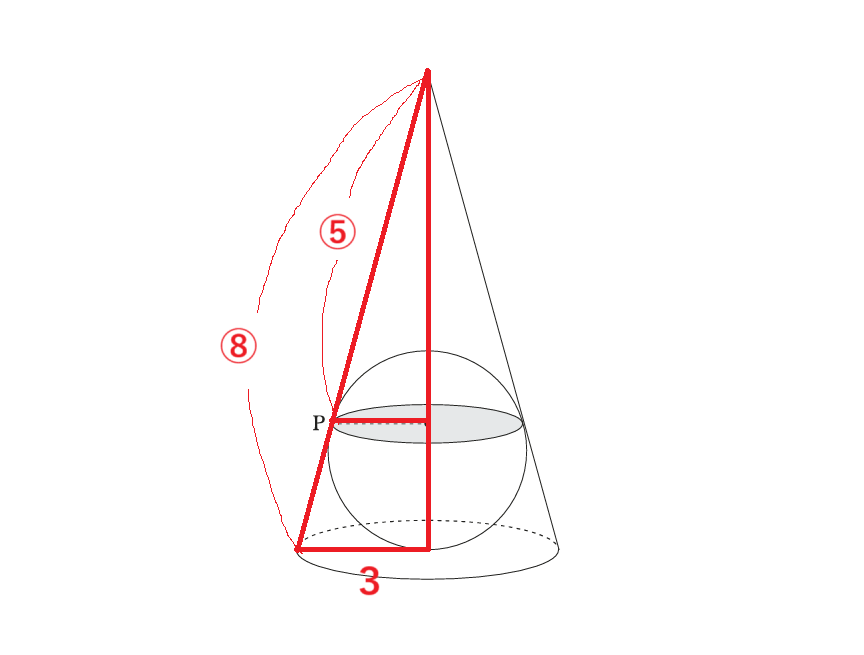
よって切り口の面積は、3×5/8=15/8を半径とする円の面積となる。
よって答えは225π/64となる。