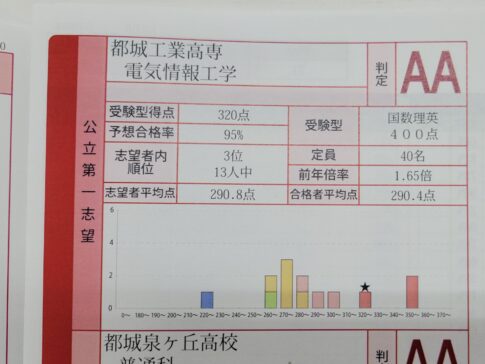
先週、夏の模試が終わりました。あとは結果待ちの状態です。
そして、模試や学校のテストは「受けた後が大事」になってきます。

解けなかった問題を「解き直す」作業ですね。
ニガテな単元はそのままにしがちなので、解き直しをするかどうかで学力に差がつきます。
問題が解けなかった理由も、いろいろあると思います
例えば数学なら、
- 計算ミス
- 公式を忘れていた
- 時間が足りなかった
- 完全にか分からなかった
などでしょうか。
この中で「完全に分からなかった」以外は、割りとすぐに直すことができます。
まずはすぐに直せるところを中心に直していきましょう。
そのあとに「完全に分からなかった」をどうするかですね。
完全に分からない問題(単元)は「分かるところから」再スタート
完全に分からなかった問題も、直す必要がある問題と直す必要がない問題に分かれます。
例えば、自分の志望校から考えて明らかにハイレベルの問題ですね。
これは合格に必要ない問題なので、無理して解き直す必要はありません。
塾では「解く問題」と「解かなくて良い問題」とに分けて指導しているので、塾生はこの辺りは判別できると思います。
しかし、
大問の上の問題や、正解率が高い問題は「必ず解く」必要があります。
完全に分からない時は、分かる位置まで戻って学習します。
連立方程式が分からないなら、方程式から再スタートする。
方程式の分数の計算が分からないなら、小学生の分数からスタートする。
このように基礎からの再スタートは遠回りのようですが、高校入試で必ず力を発揮してくれます。
自塾では自動的に弱点を見つけだし、分かる位置からスタートできるシステムになっているので基礎につまずきのある方にオススメです!