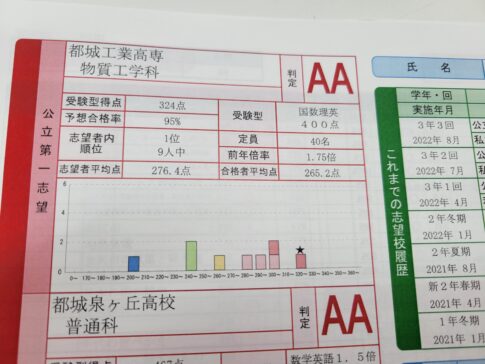
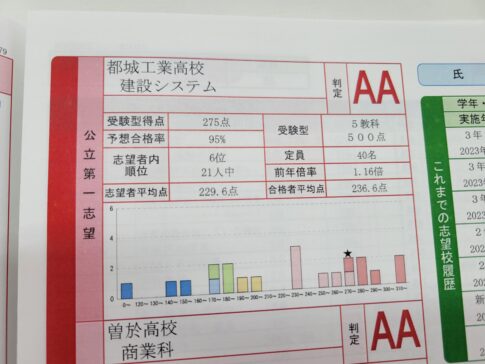
塾長が勝手に過去問を解いて解説するコーナーです。
解説が豊富な過去問は解きません。今回は高専の追試験の過去問です。
追試験は解説が載っていないはずなので、過去問やってみたけど解き方が分からない方がいたら参考にしてください。
受験生は二次関数まで終わっていたらチャレンジできます!
さっそく高専の過去問を解いてみよう
スマホだと見えずらいでしょうか?
ちゃんとプリントで解きたい方は、高専の公式ホームページから過去問3年分ダウンロードできますよ。高専ホームページ
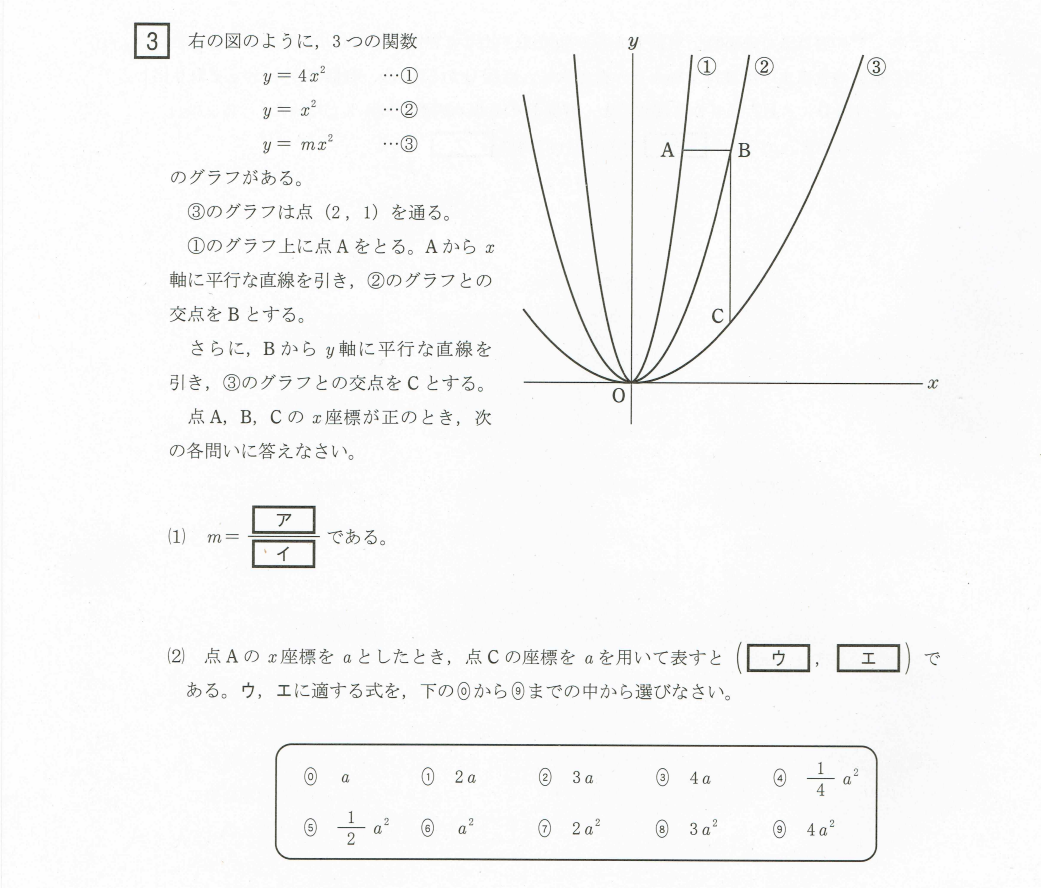
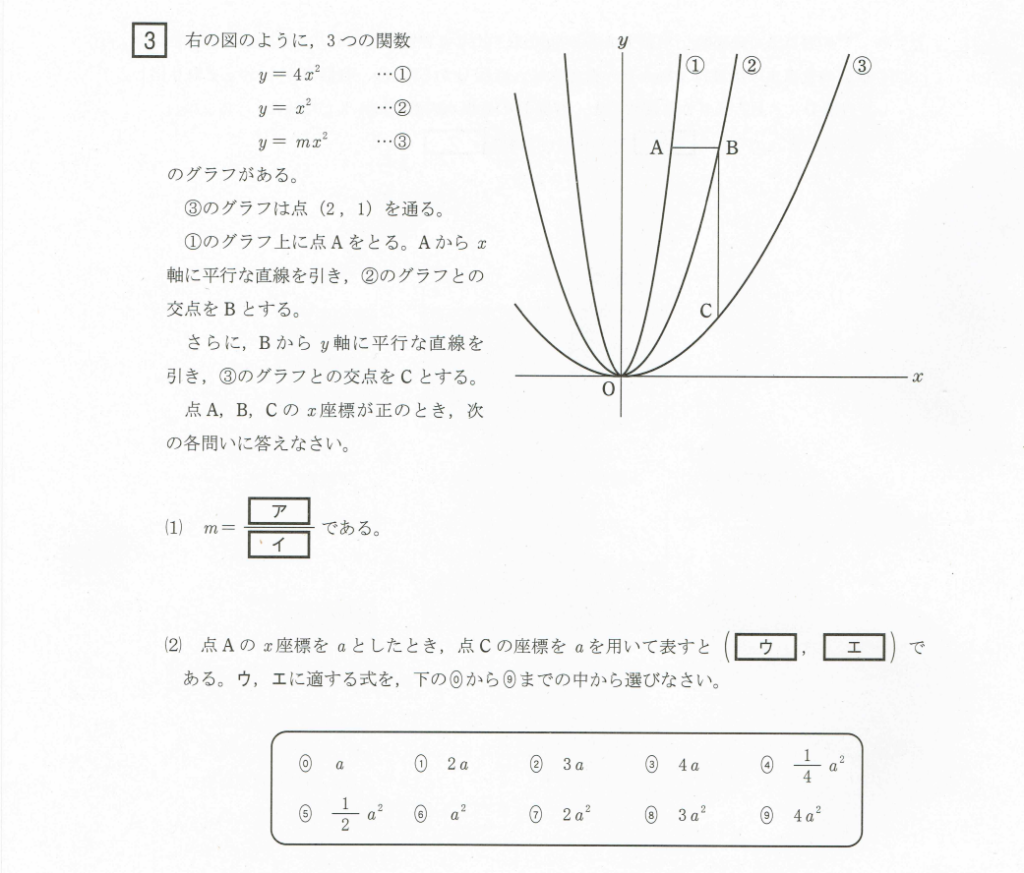
(1)変化の割合を求める
(1)はウォーミングアップ問題です。
【解説】
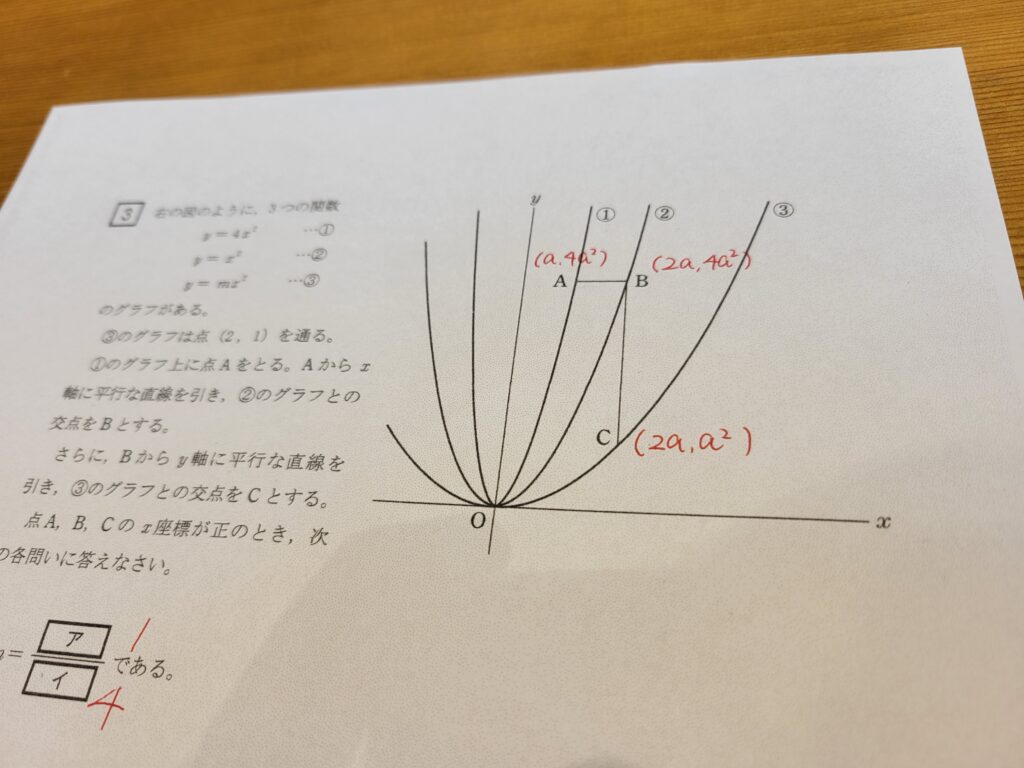
③のグラフは点(2,1)を通っているのが分かっているので、xとyにそれぞれ代入。
1=4m となり、m=1/4
ア=1 イ=4
(2)文字を使って点Cの座標を表す
(2)は文字を使った問題ですね。文字を使った問題がニガテな方は、文字を使った過去問を10問以上解くと慣れてきますよ。
【解説】
①のグラフはy=4x²なので、xのところにaを代入。
するとy=4a²となる。点Aと点Bは平行なので、②のグラフのyに4a²を代入。
4a²=x² となるので、両辺に根号をつけて、x=2a
点Bと点Cは垂直なので、BとCのx座標は等しくなる。
よってCのx座標は2a。
③のグラフのxに2aを代入して、y=a²
ウ=2a エ=a²
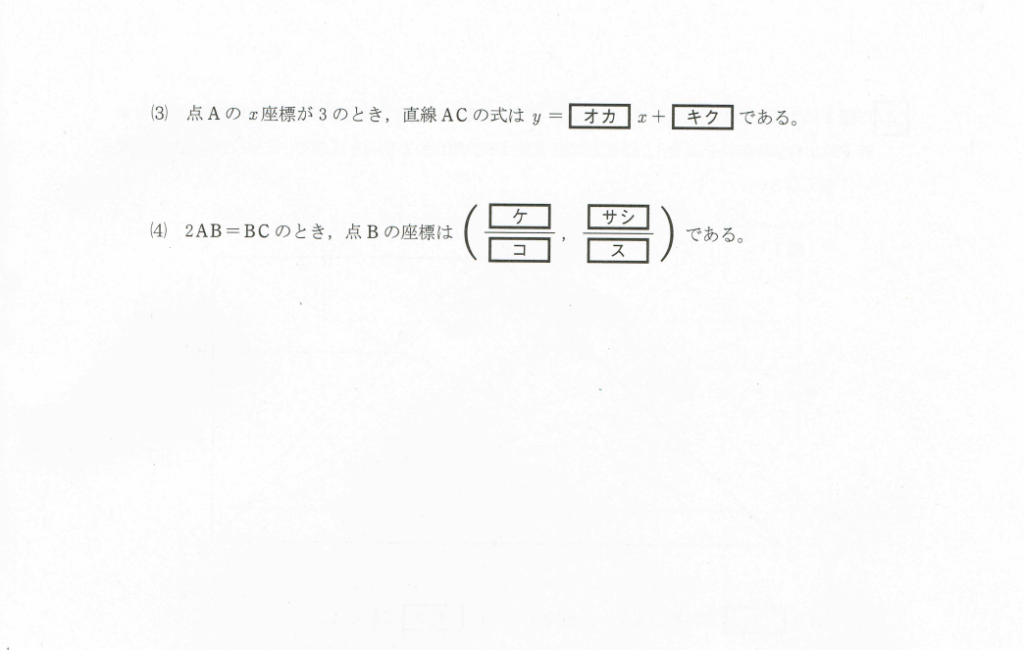
(3)直線ACの式を求める
(3)計算ミスに気をつければ解ける問題です。
【解説】
点Aのx座標が3なので、点Aの座標は(3,36)
点Bの座標は(6,36)になるので、点Cの座標は(6,9)
点Aから点Cまで、xは3増加している。
点Aから点Cまで、yは27減少している。
よって直線の傾きはー27/3より、-9
y=-9x+b に点Cの座標を代入して、b=63
オカ=-9 キク=63
(4)ラスボスは時間内に解けるかどうか
(4)ここまできたら時間との戦いです。
(2)の問題で、aを使ってそれぞれの点の座標を求めているので、ここでもaを使いましょう。
【解説】
2AB=BC になれば良いので、まずはABとBCそれぞれの辺の長さをaを使って求める。
AB=点Bのx座標-点Aのx座標なので、2a-a=a
BC=点Bのy座標ー点Cのy座標なので、4a²ーa²=3a²
AB=a、BC=3a²が分かったので、2AB=BCに代入。
すると2a=3a²になるので、両辺をaで割ってa=2/3
これを点Bの座標に代入。座標は(4/3、16/9)になる。
ケ=4、コ=3 サシ=16、ス=9
高専の関数は正確に、スピーディーに!
いかがでしたか?
高専の関数は、やや面倒な計算が多いのが特徴です。
最後の問題まで焦って解こうとせずに、スピードを意識しながらも取れる問題を確実に取ってくださいね。